


Next: Star Cluster Evolution
Astrophysics on the GRAPE Family of Special Purpose Computers
Piet Hut
Institute for Advanced Study
Princeton, NJ 08540, U.S.A.
Jun Makino
Department of General Systems Study
College of Arts and Sciences, University of Tokyo
3-8-1 Komaba, Meguro-ku, Tokyo 153-8902, Japan
Abstract:
The GRAPE-4, the world's fastest computer in 1995-1997, has produced
some major scientific results, through a wide diversity of large-scale
simulations in astrophysics. Applications have ranged from planetary
formation, through the evolution of star clusters and galactic nuclei,
to the formation of galaxies and clusters of galaxies.
Computational physics has emerged as a third branch of physics,
grafted onto the traditional pair of theoretical and experimental
physics. At first, computer use seemed to be a straightforward
off-shoot of theoretical physics, providing solutions to sets of
differential equations too complicated to solve by hand. But soon the
quantitative improvement in speed yielded a qualitative shift
in the nature of these computations. Rather than asking particular
questions about a model system, we now use computers more often to
model the whole system directly. Answers to relevant questions are
then extracted only after a full simulation has been completed. The
data analysis following such a virtual lab experiment is carried out
by the computational physicist in much the same way as it would be
done by an experimenter or observer analyzing data from a real
experiment or observation.
Recent increase in computer speed is already significantly more modest
than what could be expected purely from the ongoing miniaturization of
computer chips. Since the number of transistors on a single chips
doubles every  years, a chip now contains a hundred times more
transistors than it did ten years ago. With a clock speed increase of
more than a factor ten, one might have expected a speed increase of
more than a factor thousand, over the last decade. However, the
actual speed increase of a typical computer chip has been at most a
factor hundred, lagging far behind theoretical expectations. The
reason for this relatively poor performance lies in the significant
overhead caused by the growing complexity of a general-purpose chip.
Hence, designing a chip for only one specific purpose yields a
rapidly growing pay-off. Therefore, the time seems ripe to explore
which types of calculations can be realized directly in hardware, in
the form of special-purpose computers, rather than run in software on
general-purpose computers.
years, a chip now contains a hundred times more
transistors than it did ten years ago. With a clock speed increase of
more than a factor ten, one might have expected a speed increase of
more than a factor thousand, over the last decade. However, the
actual speed increase of a typical computer chip has been at most a
factor hundred, lagging far behind theoretical expectations. The
reason for this relatively poor performance lies in the significant
overhead caused by the growing complexity of a general-purpose chip.
Hence, designing a chip for only one specific purpose yields a
rapidly growing pay-off. Therefore, the time seems ripe to explore
which types of calculations can be realized directly in hardware, in
the form of special-purpose computers, rather than run in software on
general-purpose computers.
One of these projects has resulted in the GRAPE (short for GRAvity
PipE) family of special-purpose hardware, designed and built by a
small group of astrophysicists at the University of Tokyo
[1]. Like a graphics accelerator speeding up
graphics calculations on a workstation, without changing the software
running on that workstation, the GRAPE acts as a Newtonian force
accelerator, in the form of an attached piece of hardware. In a
large-scale gravitational N-body calculation, where N is the
number of particles, almost all instructions of the corresponding
computer program are thus performed on a standard workstation, while
only the gravitational force calculations, in innermost loop, are
replaced by a function call to the special-purpose hardware.
Specifically, the force integration and particle pushing are all done
on the host computer, and only the inter-particle force calculations
are done on the GRAPE (fig. 1). This may seem problematic, given the
fact that the intrinsic speed of the GRAPE is a factor of 10,000 times
larger than that of the host computer, an ordinary workstation.
However, the inter-particle calculations require a computer processing
power that scales with 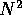 , while all other actions on the host
scale only in proportion to N. Therefore, each doubling of the
number of particles doubles the work load on the GRAPE, relative to
that of the workstation. In this way, no matter how slow the
workstation is, it will be able to keep up with the GRAPE for large
enough values of N.
, while all other actions on the host
scale only in proportion to N. Therefore, each doubling of the
number of particles doubles the work load on the GRAPE, relative to
that of the workstation. In this way, no matter how slow the
workstation is, it will be able to keep up with the GRAPE for large
enough values of N.
For some applications, more efficient algorithms have been deviced,
that require the computation of a number of inter-particle force
calculations that scales with  , rather than
, rather than 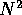 . It turns
out that even these methods can still be efficiently run on the GRAPE
[2]; although the asymptotic scaling advantage is not
very large in that case, the overall coefficient in the scaling
relation turns out to favor the use of the GRAPE. Some versions of
the GRAPE (Table 1) allow arbitrary force implementations, for
applications such as molecular dynamics. For example, the MDGRAPE has
been used to study the structure of protein molecules [3].
However, most GRAPEs have been used to study astrophysical problems.
Below we will review a few representative cases.
. It turns
out that even these methods can still be efficiently run on the GRAPE
[2]; although the asymptotic scaling advantage is not
very large in that case, the overall coefficient in the scaling
relation turns out to favor the use of the GRAPE. Some versions of
the GRAPE (Table 1) allow arbitrary force implementations, for
applications such as molecular dynamics. For example, the MDGRAPE has
been used to study the structure of protein molecules [3].
However, most GRAPEs have been used to study astrophysical problems.
Below we will review a few representative cases.

Figure 1: The GRAPE-4 hardware.

Table 1: Summary of GRAPE Hardware ([1])



Next: Star Cluster Evolution
Jun Makino
Thu Nov 26 22:13:16 JST 1998
 years, a chip now contains a hundred times more
transistors than it did ten years ago. With a clock speed increase of
more than a factor ten, one might have expected a speed increase of
more than a factor thousand, over the last decade. However, the
actual speed increase of a typical computer chip has been at most a
factor hundred, lagging far behind theoretical expectations. The
reason for this relatively poor performance lies in the significant
overhead caused by the growing complexity of a general-purpose chip.
Hence, designing a chip for only one specific purpose yields a
rapidly growing pay-off. Therefore, the time seems ripe to explore
which types of calculations can be realized directly in hardware, in
the form of special-purpose computers, rather than run in software on
general-purpose computers.
years, a chip now contains a hundred times more
transistors than it did ten years ago. With a clock speed increase of
more than a factor ten, one might have expected a speed increase of
more than a factor thousand, over the last decade. However, the
actual speed increase of a typical computer chip has been at most a
factor hundred, lagging far behind theoretical expectations. The
reason for this relatively poor performance lies in the significant
overhead caused by the growing complexity of a general-purpose chip.
Hence, designing a chip for only one specific purpose yields a
rapidly growing pay-off. Therefore, the time seems ripe to explore
which types of calculations can be realized directly in hardware, in
the form of special-purpose computers, rather than run in software on
general-purpose computers.
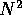 , while all other actions on the host
scale only in proportion to N. Therefore, each doubling of the
number of particles doubles the work load on the GRAPE, relative to
that of the workstation. In this way, no matter how slow the
workstation is, it will be able to keep up with the GRAPE for large
enough values of N.
, while all other actions on the host
scale only in proportion to N. Therefore, each doubling of the
number of particles doubles the work load on the GRAPE, relative to
that of the workstation. In this way, no matter how slow the
workstation is, it will be able to keep up with the GRAPE for large
enough values of N.
 , rather than
, rather than 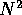 . It turns
out that even these methods can still be efficiently run on the GRAPE
[
. It turns
out that even these methods can still be efficiently run on the GRAPE
[
