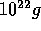 , where the runaway growth
takes place. Here we consider the smaller mass range, where the
evolution is more complex.
, where the runaway growth
takes place. Here we consider the smaller mass range, where the
evolution is more complex.
Up to here, we discussed the mass function of planetesimals for the
mass range higher than 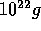 , where the runaway growth
takes place. Here we consider the smaller mass range, where the
evolution is more complex.
, where the runaway growth
takes place. Here we consider the smaller mass range, where the
evolution is more complex.
WetherillStewart1993 performed extensive simulations using
a particle-in-a-box approach, which included both the coagulation and
fragmentation, and obtained the mass function. Their result did not
depend on the details of the calculation and could be summarized as
follows: For the mass range 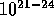 , the power index is
close to
, the power index is
close to 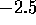 , in good agreement with our analytical result. For
smaller mass, it seems that the power index is approximately
, in good agreement with our analytical result. For
smaller mass, it seems that the power index is approximately 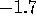 .
.
For this low-mass region, we can assume that evolution in their
simulation is dominated by the fragmentation process. The formalism of
Tanakaetal1996 can also be used for this case. Here,
however, the collision rate P has a power index different from that
for the runaway growth region, because the equipartition of energy is
not established and gravitational focusing is not effective. Thus,
relative velocity is independent of the mass and collision cross
section is geometrical. Therefore we have 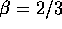 and
and 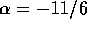 . This result is in fair agreement with the numerical result of
WetherillStewart1993, for the intermediate mass range
(
. This result is in fair agreement with the numerical result of
WetherillStewart1993, for the intermediate mass range
(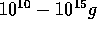 ). This value of
). This value of 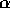 is the same as
that for the collisional cascade [], because in
both cases the collision cross section is geometrical.
is the same as
that for the collisional cascade [], because in
both cases the collision cross section is geometrical.
For even smaller masses, they obtained a somewhat shallower slope. This is the natural result of the positive dependence of the velocity dispersion on the mass due to strong gas drag.
Using an exact analytic treatment, we obtained the power-law mass distribution of planetesimals which has been found in numerical simulations of runaway growth. The mechanism through which the power-law distribution is realized is directly related to the occurrence of runaway growth, where heavier planetesimals grow faster than lighter planetesimals.
Our treatment of runaway growth is different from
those in previous theoretical works (see,  , Ohtsuki and Ida
1990, Ida and Makino 1992a, 1992b), where the growth rate was obtained for different planetesimals in the background
distribution of single-mass planetesimals. In those analyses, the
difference in the growth rates can come only from the difference in the
mass of the planetesimals under consideration. In other words,
previous works dealt with the growth of the small perturbation of the
mass from the uniform distribution (linear stability analysis).
, Ohtsuki and Ida
1990, Ida and Makino 1992a, 1992b), where the growth rate was obtained for different planetesimals in the background
distribution of single-mass planetesimals. In those analyses, the
difference in the growth rates can come only from the difference in the
mass of the planetesimals under consideration. In other words,
previous works dealt with the growth of the small perturbation of the
mass from the uniform distribution (linear stability analysis).
In the present work, we investigated the evolution of the mass distribution function which is far from uniform, taking into account the non-uniformity of the background distribution as well. As a result, we were able to derive the stationary distribution, which is consistent with the result of numerical experiments.
Our result suggests that the power-law mass distribution of
planetesimals is a universal law which is realized in the early stage
of runaway growth. Since the evolution of the
mass function in the late runaway stage is quite slow
[,], we can conclude that the
distribution of the mass of planetesimals follows this power law for most of the planet
formation period. The mass distribution for smaller masses (less than
 ) is expressed by a different power law, since in this regime
energy equipartition is not established.
) is expressed by a different power law, since in this regime
energy equipartition is not established.