


Next: 5 Discussions
Up: Yet another fast multipole
Previous: 3 Pseudoparticle Multipole Method
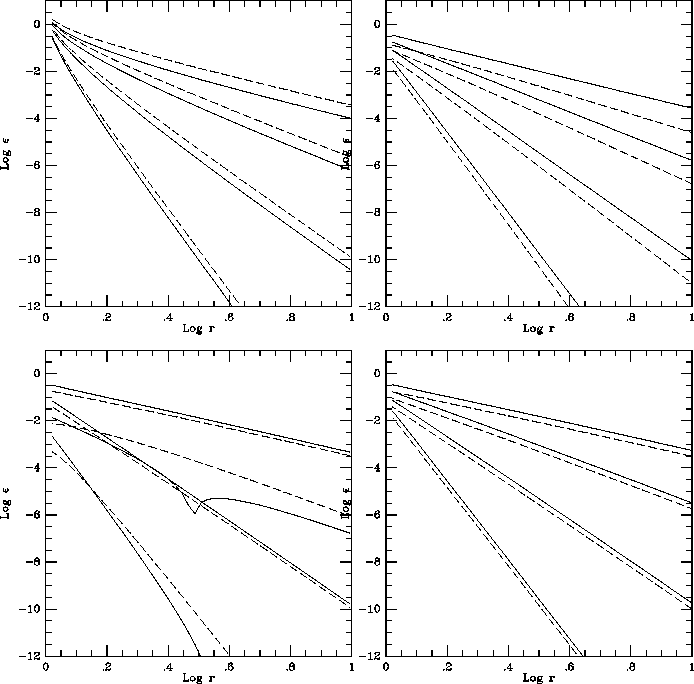
Figure 2: The absolute error of potential calculated using classical
FMM and the pseudoparticle method. The error of the potential by one
particle at position (1,0) is plotted as the function of the distance
of r. Solid and dashed curves denote the pseudoparticle method and
classical FMM, respectively. In each panel, four curves give the
results for p=2, 4, 8 and 16 (top to bottom). Four panels are result
for the direction angle 0 (top left),  (top right),
(top right), 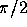 (bottom left),
(bottom left),  (bottom right), respectively.
(bottom right), respectively.
Figure 2 shows the decay of the error in two
dimensions, for various choices of expansion order and geometry. Here
we calculate the absolute error in the potential between two
particles. One is located at  . The other is located at
. The other is located at
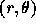 , where r is varied from 1 to 10 in each panel and
, where r is varied from 1 to 10 in each panel and
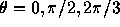 and
and  for four panels, respectively.
As is clearly seen, for all cases the new method achieves the
theoretical order. It's error is slightly larger than that of direct
evaluation of multipole expansion, but the difference is small.
for four panels, respectively.
As is clearly seen, for all cases the new method achieves the
theoretical order. It's error is slightly larger than that of direct
evaluation of multipole expansion, but the difference is small.
Note that we could make the result obtained by the new method to be
identical to the direct evaluation of multipole expansion, by
truncation the pairwise potential to the order of the integration
scheme p. However, the result shown in figure 2
suggests such truncation is unnecessary.
One practical problem is how we chose the radius of the ring. Though
the expansion is exact up to order p, a ring of finite number of
particles and finite radius has spurious high-order multipole
moment. Therefore, in order to make the truncation error small, we
should make the radius as small as possible. On the other hand, as we
make the radius r smaller, the absolute values of the masses of
particles diverge as 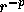 , since this factor directly enters into
the inverse transformation. Therefore, if we make r too small, the
round off error would increase rapidly. In practice, the choice of
, since this factor directly enters into
the inverse transformation. Therefore, if we make r too small, the
round off error would increase rapidly. In practice, the choice of
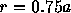 makes the spurious high-order terms sufficiently small,
without noticeable effect on the round-off error. For the result shown
in figure 2 we used
makes the spurious high-order terms sufficiently small,
without noticeable effect on the round-off error. For the result shown
in figure 2 we used 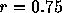 . The error is not
sensitive to the choice of r, unless the required accuracy is very
high.
. The error is not
sensitive to the choice of r, unless the required accuracy is very
high.



Next: 5 Discussions
Up: Yet another fast multipole
Previous: 3 Pseudoparticle Multipole Method
Jun Makino
Tue Feb 16 23:27:09 JST 1999

 (top right),
(top right), 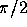 (bottom left),
(bottom left),  (bottom right), respectively.
(bottom right), respectively. . The other is located at
. The other is located at
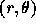 , where r is varied from 1 to 10 in each panel and
, where r is varied from 1 to 10 in each panel and
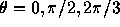 and
and  for four panels, respectively.
As is clearly seen, for all cases the new method achieves the
theoretical order. It's error is slightly larger than that of direct
evaluation of multipole expansion, but the difference is small.
for four panels, respectively.
As is clearly seen, for all cases the new method achieves the
theoretical order. It's error is slightly larger than that of direct
evaluation of multipole expansion, but the difference is small.
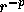 , since this factor directly enters into
the inverse transformation. Therefore, if we make r too small, the
round off error would increase rapidly. In practice, the choice of
, since this factor directly enters into
the inverse transformation. Therefore, if we make r too small, the
round off error would increase rapidly. In practice, the choice of
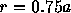 makes the spurious high-order terms sufficiently small,
without noticeable effect on the round-off error. For the result shown
in figure
makes the spurious high-order terms sufficiently small,
without noticeable effect on the round-off error. For the result shown
in figure 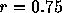 . The error is not
sensitive to the choice of r, unless the required accuracy is very
high.
. The error is not
sensitive to the choice of r, unless the required accuracy is very
high.