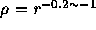 , where
, where 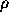 is the volume luminosity
density.
is the volume luminosity
density.
In this section, we briefly describe our resent work on the massive central black holes in the centers of galaxies (Makino and Ebisuzaki [1996], Makino [1997], Nakano and Makino [1999a,1999b]). The problem is what happens when two galaxies, each with a central black hole, merge. The merging of two galaxies is a rather common event. According to the standard scenario of the structure formation in the universe (hierarchical gravitational clustering), galaxies are constructed ``bottom up'' from smaller objects through merging. On the other hand, almost all galaxies except for some dwarfs seem to have central black holes. Thus, if two such galaxies merge, the merger remnant would have two black holes. These black holes would settle in the center of the merger remnant, and would eventually form a binary. Two questions arise: (a) What is the structure of the central region of the merger galaxy with two black holes? and (b) What will happen to the binary itself? Will two black holes eventually merge?
Makino and Ebisuzaki ([1996]) studied the first
problem, assuming that black holes would eventually merge. They
performed the simulation of hierarchical (repeated) merging similar
to those by Farouki et al. ([1983]), but with central
black holes. What Farouki et al. found is that the core radius
remains almost unchanged after merging, even though the half-mass radius
almost doubles after each merging event. This result is consistent
with the theoretical prediction based on the conservation of the
central phase space density, but in complete contradiction with the
observations of luminous elliptical galaxies. Ground-based
observations in 1980s demonstrated that there is strong correlation
between the effective radius and the ``core'' radius of luminous
ellipticals (Lauer [1985]). HST observations (Gebhaldt
et al. [1996])
have shown that the ``cores'' are actually all cusps with the profile
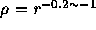 , where
, where 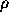 is the volume luminosity
density.
is the volume luminosity
density.
Figure 7 show the result of simulations with GRAPE-4. The central region of the merger with central black hole looks like the shallow cusps observers found in luminous ellipticals, and the radius of this cusp region is a constant fraction of the half-mass radius. Thus, numerical simulations of merging of galaxies with black holes reproduced the observed characteristic of the central regions of luminous ellipticals rather well.
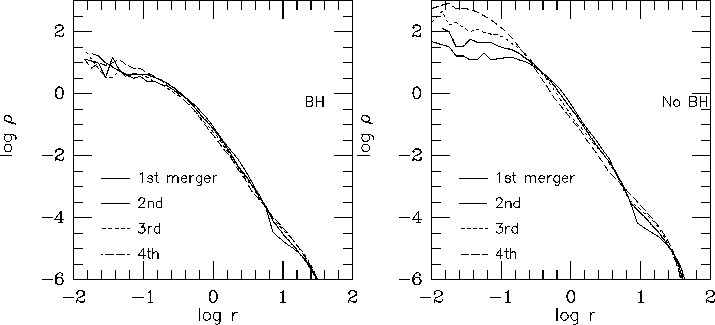
Figure 7: The density profiles of the mergers with central black
holes. Profiles are scaled so that the half-mass radii are the same
for all remnants. The panel in the left side shows the results of runs
with central black holes, and that in the right without black holes. Reproduced from Makino and Ebisuzaki (1997).
Nakano and Makino ([1999a,1999b])
investigated why the cusp is formed. First, they tried to understand
the formation mechanism better by means of simplified experiments, in
which just one black hole was let to sink to the center of a
galaxy. Except for the case that the black hole is originally in the
center, the cusp with  is universally formed, and the
mass within the cusp region is comparable to that of the mass of the
central BH.
is universally formed, and the
mass within the cusp region is comparable to that of the mass of the
central BH.
In the second paper (Nakano and Makino 1999b), they came
up with a simple explanation for the formation mechanism. The
black hole sink to the center through the dynamical friction, in the
dynamical timescale. When the black hole settled at the center of the
galaxies, almost no star was strongly bound to the black hole. This is
because the black hole sinks to the center relatively slowly. The
sinking timescale is not so slow that the adiabatic approximation can
be applied to the binding energy of the stars, but sufficiently slow that
the binding energy of most of the stars does not change very much.
Thus, the distribution function 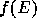 has a sharp cutoff at the
energy close to the central potential depth of the initial galaxy
model.
has a sharp cutoff at the
energy close to the central potential depth of the initial galaxy
model.
If there is a central massive object and  has a sharp cutoff, we
can show that the central region is a cusp with the slope
has a sharp cutoff, we
can show that the central region is a cusp with the slope  as
follows.
as
follows.
The density is obtained by integrating the distribution function in the velocity space as follows:
where  is the potential at distance r from the center,
where the black hole lies. Note that we assumed that the velocity
distribution is isotropic.
is the potential at distance r from the center,
where the black hole lies. Note that we assumed that the velocity
distribution is isotropic.
We assume that  if
if 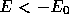 . For any r with
. For any r with 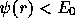 , equation (2)
can be rewritten as
, equation (2)
can be rewritten as
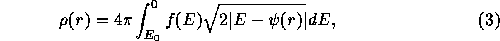
which can be expanded as
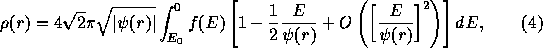
Therefore, we have
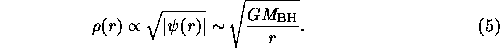
For the fate of the black hole binary, we performed simulations with
very wide range of the number of particles (2,048 to 262,144) to investigate
the dependence of the growth timescale of the binding energy of the
binary on the number of particles in the galaxy. What we found was
intriguing. The timescale seemed to be proportional to 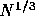 ,
while, theoretically, the timescale must be proportional to N, since
the timescale should be limited by the timescale of filling the loss
cone through two-body relaxation. We have not yet understood why our
numerical experiments did not agree with the theoretical
prediction. Simulations with larger N, which will be possible with
GRAPE-6, will give us important clues for the understanding of this
problem.
,
while, theoretically, the timescale must be proportional to N, since
the timescale should be limited by the timescale of filling the loss
cone through two-body relaxation. We have not yet understood why our
numerical experiments did not agree with the theoretical
prediction. Simulations with larger N, which will be possible with
GRAPE-6, will give us important clues for the understanding of this
problem.